CeldyFEM Background: Theory behind.

The geometric shape

In CeldyFEM, each cell is represented as a set of some points and inner triangulation mesh. The cell's elastic features such as Young's modulus and poisson ratio are assigned to each triangle element.

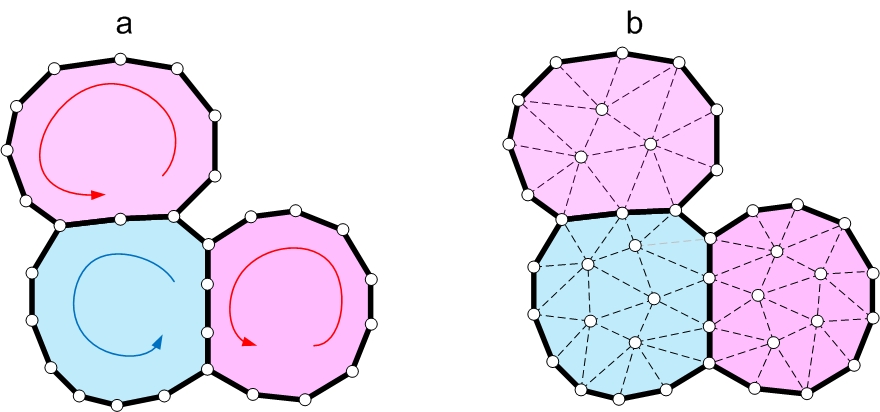
Discretization of cells. (a) An example of a toy tissue consisting of three cells. The boundary of each cell is defined by a counter-clock wise oriented polygon containing a number of boundary vertices. (b) Triangular mesh tiling up each cell is generated using the farthest point sampling method.

Cell proliferation and migration

Cells are deformed according to internal or external forces due to different behaviors. (a) Cell proliferation is driven by the internal pressure force. (b) Cell migration is driven by the protrusion force generated from actin polymerization.

Cell adhesion

The finite element method is used to get the cell deformation. The elastic contraction forces are then recovered at each cell boundary vertex. This can be used to test the rupture of cell-cell adhesions.

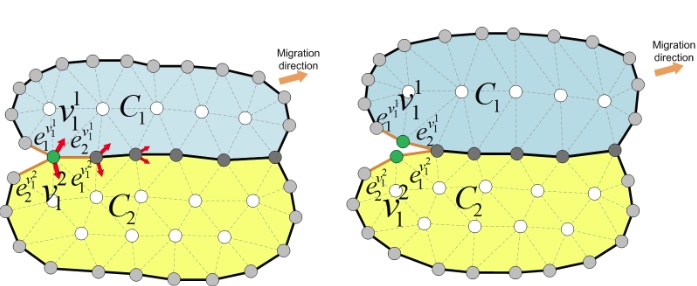
Contractile forces are recovered to break intercellular adhesion.

Geometric correction

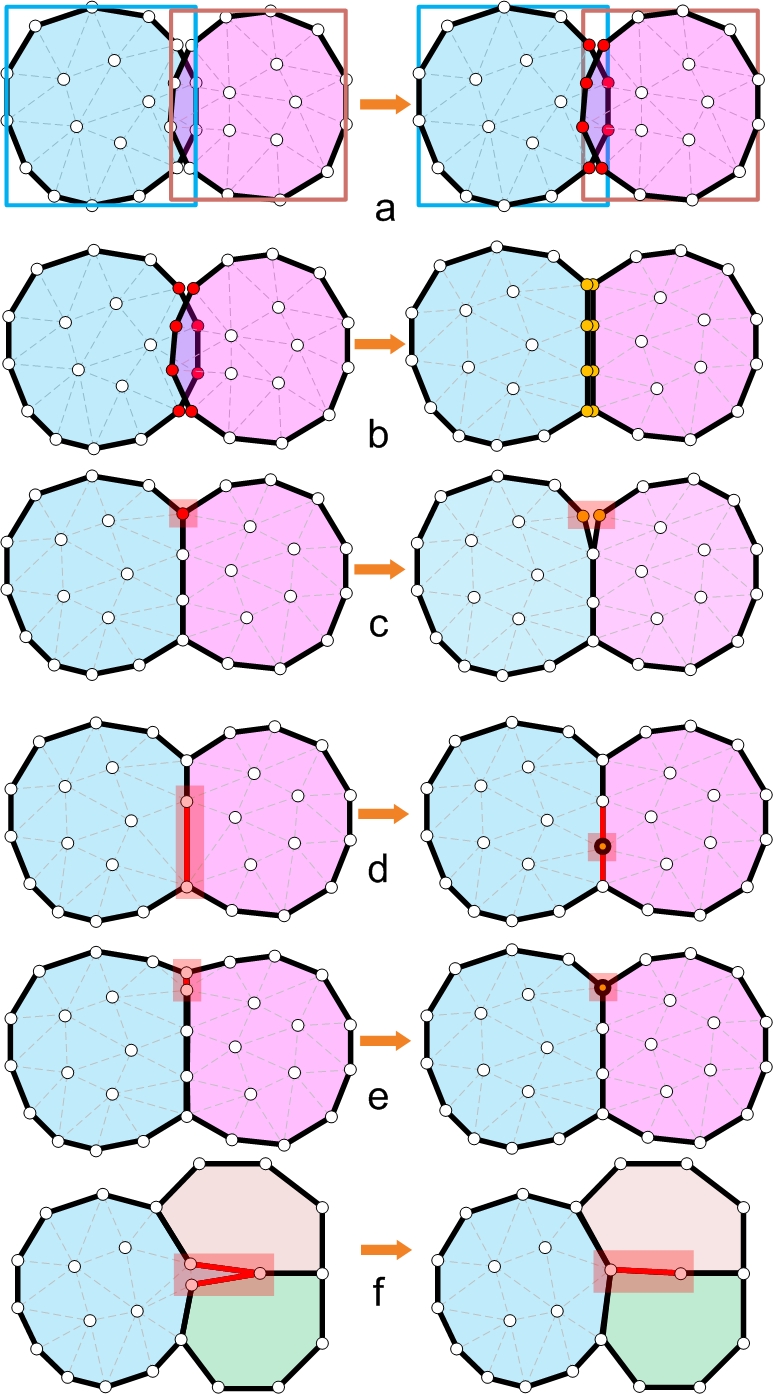
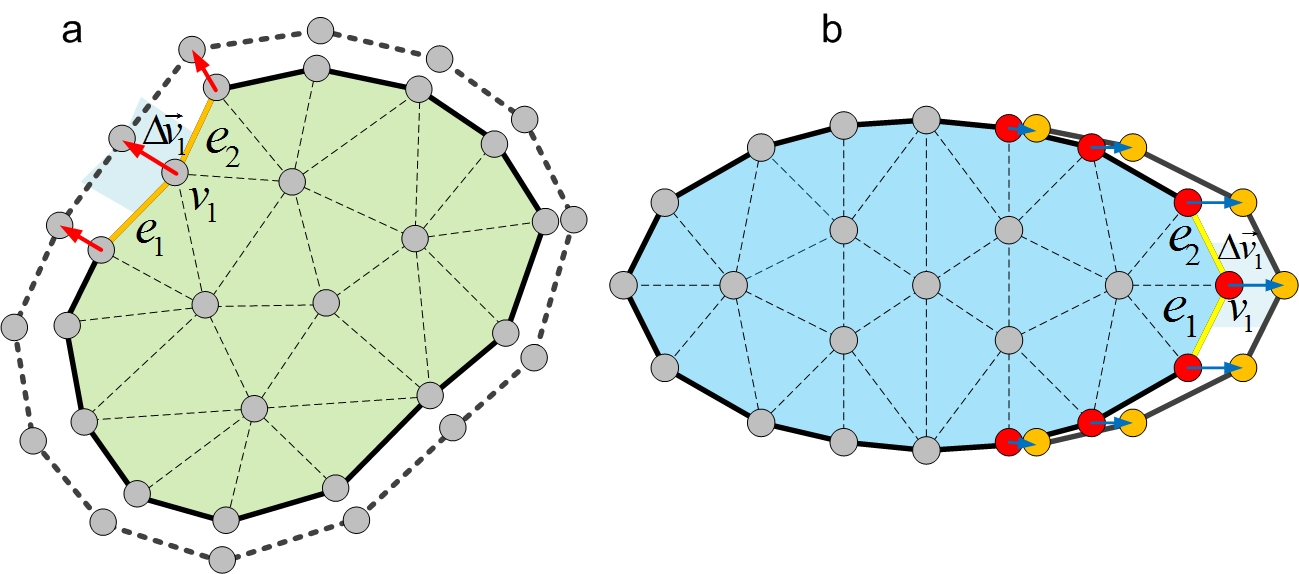
It is important to detect collision when the bodies of two cells start to overlap and compute the contacting surface of cells properly.

(a) Intersection of two bounding boxes of cells fro collision detection: the overlapping surfaces of the two colliding cells are identified upon examining the intersection of the two bounding boxes. (b) Collision between two cells is detected and repaired by constructing the initial contacting surface. (c) Previously attached vertices on the contacting surfaces of two different cells are separated from each other. (d) When an edge becomes longer than a predefined threshold, it is subdivided by adding a new vertex at the midpoint. (e) When an edge becomes shorter than a predefined threshold, it is removed from the cell. (f) When a skinny triangle with an angle smaller than a predefined threshold appears high aspect ratio of the longest edge and the shortest edge is detrimental to the numerical stability required in finite element calculation. We therefore remove this skinny triangle, two of its edges, and one of its vertices. A new edge is then added to connect the two remaining vertices.